Addition
Pronunciation: /əˈdɪ.ʃən/ ExplainAddition is joining two or more quantities together to make a sum. Figure 1 gives an example of integer addition. In the addition statement 4 + 3 = 7, 4 and 3 are addends and 7 is the sum. Addends are what is being added together, and the sum is the result of the addition. The symbol '+' is called the addition sign.
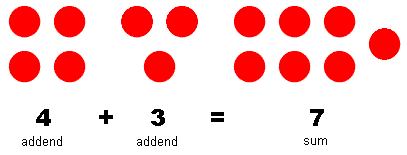 |
| Figure 1: Representation of 4 + 3 = 7 |
Real numbers can also be added. Figure 2 gives a representation of 2 + 1 = 3.
 |
| Figure 2: Representation of 2 + 1 = 3 |
Manipulative 3 represents the addition of real numbers. Click on the blue points and drag them to change the figure.
|
Click on the points A and B near the top to change the figure. The blue and red arrows on the number line show A added to B. The sum A+B is below them in purple. |
| Manipulative 1 - Addition Created with GeoGebra. |
Addition is also defined for many types of math entities such as vectors and matrices.
Subtraction
Mathematicians usually define subtraction as adding the additive inverse of a value. Subtraction is defined this way so that subtraction of vectors and matrices and other math entities makes more sense. Stated mathematically, a - b ≡ a + -b. A difference is the result of subtracting one number from another. For example, in the equation 7 - 4 = 3, 3 is the difference.
A example of this is 5 - 4 = 5 + -4 = 1
Properties of Addition of Real and Complex Numbers
| Property Name | Example | Description |
|---|---|---|
| Additive property of zero Additive identity |
a + 0 = 0 + a = a | Any number plus zero equals the original number. 0 is the additive identity for real and complex numbers. |
| Additive inverse | a + (-a) = 0 | The additive inverse of any real or complex number is the negative of that numbers. |
| Associative property of addition | a + ( b + c ) = ( a + b ) + a | The order of in which multiple additions of real and complex numbers are performed does not change the result. |
| Commutative property of addition | a + b = b + a | It doesn't matter which of two numbers come first in addition of real and complex numbers. |
| Distributive Property of Multiplication over Addition and Subtraction | a ( b + c ) = ab + ac, and a ( b - c ) = ab - ac | Multiplication is distributive over addition and subtraction. |
| Additive property of equality | If a = b then a + c = b + c. | The additive property of equality states that any number can be added to both sides of an equation without changing the truth value of the equation. |
| Subtractive property of equality | If a = b then a - c = b - c. | The subtractive property of equality states that any number can be subtracted from both sides of an equation without changing the truth value of the equation. |
| Table 1: Properties of Addition | ||
Addition Facts
Addition facts are two operands and the result of adding those two operands. The following table gives the addition facts for 0 through 10.
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 10 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
How to Add Complex Numbers
To add two complex numbers, add the corresponding parts. Given two complex numbers a + bi and c + di, (a + bi) + (c + di) = (a + c) + (b + d)i. Example: (3 - 2i) + (-1 + 3i) = (3 + (-1)) + (-2 + 3)i = 2 + 1i = 2 + i.
References
- McAdams, David E.. All Math Words Dictionary, addition. 2nd Classroom edition 20150108-4799968. pg 10. Life is a Story Problem LLC. January 8, 2015. Buy the book
Educator Resources
- McAdams, David E.. Addition of Integers Classroom Demonstrator. allmathwords.org. 12/24/2009. http://allmathwords.org/en/a/addtionintegers_cd.html.
- McAdams, David E.. Addition of Real Numbers Classroom Demonstrator. allmathwords.org. 12/24/2009. http://allmathwords.org/en/a/additionreal_cd.html.
- Addition. www.mathsisfun.com. Math Is Fun. 6/18/2018. https://www.mathsisfun.com/numbers/addition.html.
Cite this article as:
McAdams, David E. Addition. 4/5/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. http://www.allmathwords.org/en/a/addition.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/5/2019: Updated formating of equations. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/12/2018: Removed broken links, changed Geogebra links to work with Geogebra 5, updated license, implemented new markup. (McAdams, David E.)
10/12/2010: Added "Adding complex numbers", additive identity, additive inverse, and additive property of equality. (McAdams, David E.)
1/4/2010: Added "References". (McAdams, David E.)
3/3/2009: Added discussion of difference to the section on subtraction. (McAdams, David E.)
9/16/2008: Changed figure 3 to a manipulative. (McAdams, David E.)
6/7/2008: Corrected spelling errors. (McAdams, David E.)
5/14/2008: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License